Writing electron configuration

By applying the three principles, we would be able to allocate electrons into the correct orbitals. It is now our task to show our allocation using standard notations so that other people could understand.

Full notation

By using full notation, we'll start from \( 1s \) orbital and end at the last orbital with electrons. For example, we'll write

\[ 1s^22s^22p^3 \]

for nitrogen (\( N \)) which has 7 electrons in total.

It tells us that there are 2 electrons in \( 1s \) orbital, 2 electrons in \( 2s \) orbital, and 3 electrons in \( 2p \) orbital.

Let's take a closer look at the grammar using \( 2p^3 \) as our example. You'll notice that there is a \( 2 \) in front of the letter \( p \). It means \( p \) orbital in energy level 2. The superscript number \( 3 \) indicates \( 3 \) electrons in the \( 2p \) orbital.

Similarly, \( 2s^2 \) tells us that there are \( 2 \) electrons in the \( 2s \) orbital.

So can you figure out the meaning of \( 1s^2 \) then?

Here's another example, chlorine (\( Cl \)), which has a total of 17 electrons. So according to the sequence that Aufbau principle tells us,

\[ 1s \rightarrow 2s \rightarrow 2p \rightarrow 3s \rightarrow 3p \rightarrow 4s \rightarrow 3d \rightarrow 4p \]

we'll write its electron configuration as:

\[ 1s^22s^22p^63s^23p^5 \]

Isn't it simple?

But here's an even simpler way and you don't need to count the number of electrons.

The periodic table way

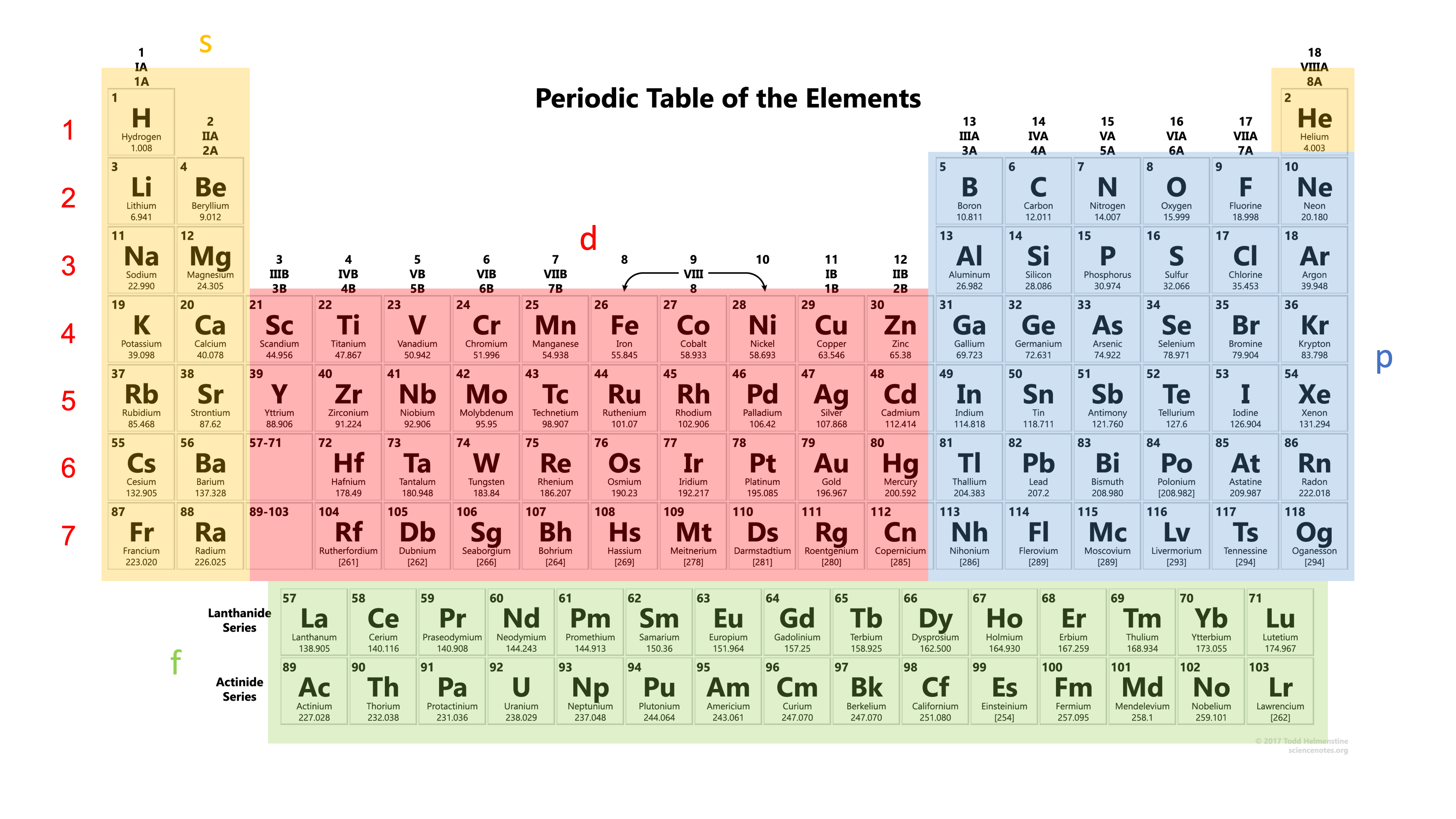
The electron configuration is actually right here in the periodic table.

First of all, the columns in the periodic table is named as Group, while the rows in the periodic table is the Period.

The two groups on the left (highlighted in yellow) make up the s block, together with the element helium (\( He \)). This is because all their electron configurations end in \( s \) orbitals.

The blue highlighted elements are in the p block. Elements in this block have their electron configurations ending with \( p \) orbitals.

The red highlighted elements make up the d block and the green highlighted elements are the f block. We'll introduce more about the periodic table and the f block in the next topic. Usually, we don't have to worry too much about the f block when writing electron configurations.

Second, the periodic table is arranged in such a way that elements with n energy levels will be placed in the \( n^{th} \) period.

For example, just now we have seen that chlorine (\( Cl \)) has an electron configuration of \( 1s^22s^22p^63s^23p^5 \), showing that the outer most occupied orbital is the \( 3p \) orbital in energy level \( 3 \). Therefore, it is placed in period 3 in the periodic table as well. Could you spot it?

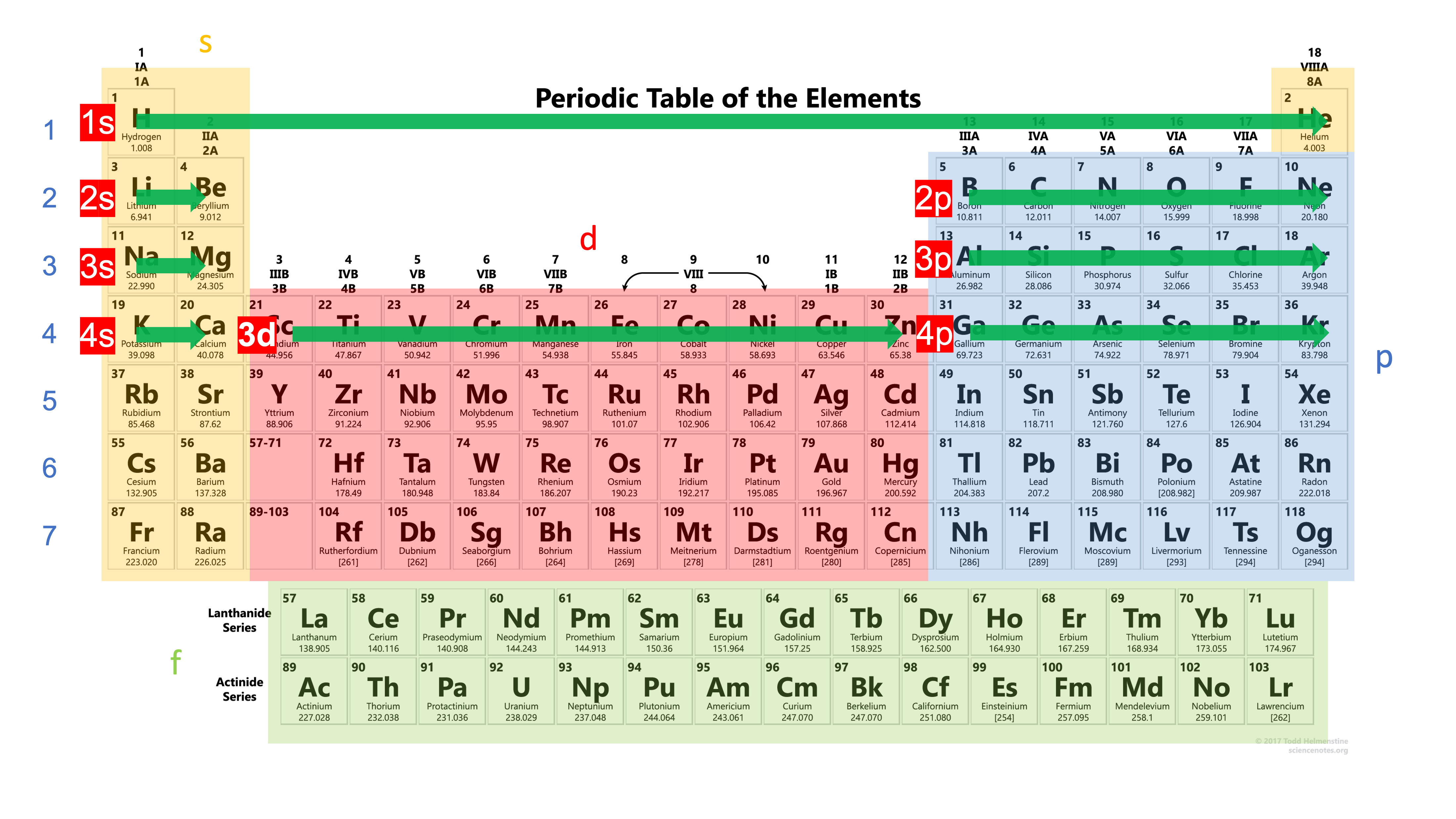
So if we look at the periodic table row by row, or period by period, from the left to the right, and combine the period number with the block, isn't it the same sequence as

\[ 1s \rightarrow 2s \rightarrow 2p \rightarrow 3s \rightarrow 3p \rightarrow 4s ... \]

However there's one important thing we have to memorize when using this method: d block is 1 energy level lower than the period number.

Therefore, after \( 4s \), you'll see \( 3d \), and then followed by \( 4p \).

Let's try a long one, selenium \( Se \), which is in period 4, group 16. By following the periodic table, period by period, left to right, we'll write its electron configuration as:

\[ 1s^22s^22p^63s^23p^6\textcolor{#d42}{4s^23d^{10}}4p^4 \]

No more counting electrons. Simple, isn't it?

But it's still troublesome as we have to write such a long electron configuration. Let's simplify it.

Noble gas notation

In the periodic table, the last group on the right is named as noble gas. All elements in this group form gases which are exceptionally stable. These elements are so stable that they won't even react with another noble gas atom, hence they always exist as monoatomic particles.

For example, helium, there is no helium molecule (\( He_2 \)) existing naturally. Helium gas just stays in the form of atoms because \( He \) atoms are already stable and they don't have to bind to another \( He \) atom to achieve stability, unlike oxygen (\( O_2 \)) or nitogen gases (\( N_2 \)) whereby single \( O \) or \( N \) atom is very unstable so they must form diatomic molecules in order to survive.

Noble gas elements are stable due to their full shell electron configurations. Their outer most energy level, the valence shell, is always fully occupied.

Whereas for other elements, we'll fill in electrons into their valence shell after we have fully filled their inner energy levels. Thus we could say there is a noble gas core formed before we start to fill in the valence electrons.

Therefore, we could simply use the symbol of the noble gas to represent the noble gas core, and write detailed electron configurations for the valence electrons only. This would greatly reduce our workload.

Again, we use selenium as the example. We used to write:

\[ 1s^22s^22p^63s^23p^64s^23d^{10}4p^4 \]

but we know that \( 1s^22s^22p^63s^23p^6 \) is just the electron configuration of argon (\( Ar \)), which is the noble gas core of \( Se \), thus we would write:

\[ \textcolor{#d42}{[Ar]}4s^23d^{10}4p^4 \]

So to summarize, we could find the nearest noble gas before the element, write its symbol with a square bracket around it, and then follow the periodic table to write the electron configuration for the valence shell.

Two things to remind you here. First, the noble gas core must be the noble gas element before. For example, if you want to write electron configuration of chlorine, use \( Ne \) instead of \( Ar \) as the noble gas core, because \( Ar \) has more electrons than \( Cl \) and you can't show removing electrons in electron configuration.

Second, once you've figured out the noble gas core and want to continue with the valence electrons using the periodic table, start from the next box in the periodic table instead of \( 1s \). So for chlorine, after \( Ne \), look at \( Na \), which is \( 3s \), and then \( 3p \). Never write \( [Ne]1s^22s^2... \). That's incorrect.

By the way, you may swap the position of \( 4s \) and \( 3d \). For example, the electron configuration of scandium \( Sc \) could be writen as either

\[ [Ar]4s^23d^1 \]

or

\[ [Ar]3d^14s^2 \]

Box notation

Sometimes we want to know the exact locations of electrons in degenerated orbitals. This could be done using the box notation.

We use boxes to represent orbitals, and orbitals from different sublevels should be drawn separately while degenerated orbitals (those from the same sublevel) should be connected together.

So for \( Sc \), scandium, we would write:

\[ \displaylines{ [Ar] \text{ } \boxed{ \text{ } \upharpoonleft \downharpoonright \text{ }} \text{ } \boxed{ \text{ } \upharpoonleft \text{ } \mid \text{ } \text{ } \text{ } \text{ } \text{ } \mid \text{ } \text{ } \text{ } \text{ } \text{ } \mid \text{ } \text{ } \text{ } \text{ } \text{ } \mid \text{ } \text{ } \text{ } \text{ } \text{ } } \newline \text{4s} \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{3d} \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } } \]

This could clearly show us how electrons are allocated. Therefore, we have to follow Pauli's exclusion principle and Hund's rule when filling up the boxes.

It is also noteworthy that we use half arrows \( \upharpoonleft \) and \( \downharpoonright \) to represent electrons. So make sure you get all the details correctly.

Exceptions

There are two very important exceptions when writing electron configurations. These exceptions also show the importance of using box notation.

Chromium

When we write the electron configuration of chromium,

\[ [Ar] 4s^23d^4 \]

or in the box notation:

\[ \displaylines{ [Ar] \text{ } \boxed{ \text{ } \upharpoonleft \downharpoonright \text{ }} \text{ } \boxed{ \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } \mid \text{ } \text{ } \text{ } \text{ } \text{ } } \newline \text{4s} \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{3d} \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } } \]

However, the actual electron configuration would be:

\[ [Ar] 4s^13d^5 \]

or in the box notation:

\[ \displaylines{ [Ar] \text{ } \boxed{ \text{ } \upharpoonleft \text{ }} \text{ } \boxed{ \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } \mid \text{ } \upharpoonleft \text{ } } \newline \text{4s} \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{3d} \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } } \]

By transferring one electron from \( 4s \) to \( 3d \) orbital, we would be able to achieve half-filled \( d \) orbital, which is more stable as compared to the original \( 3d^4 \) configuration. This could be roughly explained by saying that the \( 3d \) orbital achieves symmetry by placing one electron in each degenerated orbital. Therefore, it balances out the repulsion forces and could be more stable.

A second reason would be that removing one of the electrons from \( 4s \) orbital reduces the repulsion between electrons in the small \( 4s \) orbital.

A third reason that this is happening is due to the small energy gap between \( 4s \) and \( 3d \) orbitals. Therefore the electron transfer is possible.

Copper

A second exception is copper (\( Cu \)). The electron configuration of copper is

\[ [Ar]4s^13d^{10} \]

The reasons are the same as those for \( Cr \). But this time, \( 3d \) orbital attains fully filled configuration which is also stable due to its symmetry in space.

Electron configurations for ions

Anions

Anions are formed by adding electrons to atoms. (Do take note that you should never remove or add protons because that changes the identity of the atom)

It is simple to write electron configurations of anions. You just need to be very careful with how many electrons there are. You would then allocate all the electrons according to the same three principles as we mentioned before.

For example, \( Cl^{-} \) shows a single negative charge on the ion, which indicates that an extra electron has been added. Therefore, there are in total 18 electrons. It is isoelectronic, i.e. having the same electron configuration as argon. So you could write its electron configuration as:

\[ [Ar] \]

or

\[ [Ne]3s^23p^6 \]

Cations

It is a little different for cations. You must start with the electron configurations of the atoms first, and then remove electron from the outer most energy level.

For example, \( Cu^+ \) has an electron configuration of

\[ [Ar]3d^{10} \]

because the positive charge is generated by removing the electron from the outer most energy level (the \(4s^1\) electron is being removed).

Another example would be \( Sc^+ \), which has an electron configuration of

\[ [Ar]4s^13d^1 \]

Do NOT remove from the right most orbital in the electron configuration. Always look for the outer most energy level, i.e. the number before the sublevel symbols.

If there are more than one occupied orbitals in the outer most energy level, then you need to follow the sequence \( f \rightarrow d \rightarrow p \rightarrow s \).

One more thing to remind you is that don't rearrange electrons.

For example, \( Fe^{2+} \) has an electron configuration of

\[ [Ar]3d^6 \]

instead of \( [Ar]4s^13d^5 \) because we simply remove electrons without rearranging.

Summary

Let's summarize all the thing we have talked about electron configuration.

First, electrons are located in orbitals, which are certain areas of energy levels and sublevels with a high probability of finding electrons.

Electrons may transit between energy levels resulting in absorption or emission of electromagnetic waves, including UV, visible lights, and IR.

We observed discrete line emission spectrum with colored lines closer at higher frequencies of lights.

This led to our understanding that energy levels are existing at specific energy only, and they converge at higher energy until the convergence limit.

Quantum mechanical model is used to describe the behaviors of electrons and their allocations within the atoms, in a more precise and accurate way.

We follow Aufbau principle, Pauli's exclusion principle, and Hund's rule to determine where to put the electrons.

Finally we write down how we fill in electrons into orbitals (electron configurations) using one of the three commonly used notations.

We could follow the periodic table to write a full notation, or use a noble gas core to simplify it. If we want to know more about the allocation of electrons within the sublevels, we may use boxes to represent orbitals while half arrows showing electrons.

When using the periodic table to write electron configurations, we do remember that in the d block, we should write the energy level of the d orbitals to be the period number minus one. This is because we fill up \( 4s \) orbital before \( 3d \).

And we shouldn't forget the two exceptions, chromium (\( Cr \)) and copper (\( Cu \)), which have \( 4s^1 \) only, so that they could attain half-filled and fully filled d orbitals respectively.

For anions, we just follow the same principles and continue allocating electrons into orbitals.

In order to write electron configurations of cations, we must write down those of the atoms first, and then start removing electrons from the outer most energy level. But we should not rearrange electrons after we've done removal.