The modern way: quantum mechanical model

Although Bohr's model works well on hydrogen atoms, it is unable to describe the electron behaviours in other atoms. For example, in a helium atom (\(He\)) where two electrons exist, the electrons would affect each other so that their movements in the atom are not the same as what Bohr's model predicts.

Despite of correctly bringing up the concepts of energy levels and electron transits, Bohr's model doesn't provide a way of understanding atoms. A more sophisticated model is needed. That's the quantum mechanical model.

Quantum physics

Quantum physics is a very complicated topic in physics. Physicists have yet to understand all aspects the particular topic. Fortunately, it is developed enough to solve our problems as chemists. So we'll simply focus on the relavant parts of quantum mechanics and try to understand atoms.

According to quantum physics, we say everything has both the characters of a particle and a wave, especially for electrons. Macroscopic substances such as a piece of paper, are exhibiting primarily the same as particles. Everything you see in your daily life is behaving in this way. We could see them at particular positions in space, and we could calculate where they are moving towards.

But for electrons, and all other things at this scale, it is a different story. Substances such as electrons would possess significant characters of waves. They're moving, changing, and even disappearing at all times.

Therefore, we won't be able to know both their exact location and their momentum at the same time. This is well known as Heisenberg's uncertainty principle. It could be expressed by a mathematics inequation

\[\Delta x \cdot \Delta p_x \ge \frac{\hbar}{2} \]

where \(\hbar \) is reduced Planck's constant.

In the inequation above, \(\Delta x\) is the uncertainty of the location of the object in \(x\) direction. For example, there is an electron at about \(1.6 \times 10^{-10} \pu{m}\) away from the nucleus, and it is moving with a velocity of \(2.18 \times 10^6 \pu{m/s}\) in a particular direction. When we try to measure its location in a more precise way, we'll realize we can't measure its velocity to that precision, maybe we can only measure its velocity to be \(2 \times 10^6 \pu{m/s}\). This imprecision is the uncertainty that we talked about in the inequation above.

It's counterintuitive we know. But no matter how hard we try, we just couldn't reduce the uncertainty of location and momentum at the same time. That's the magic of quantum physics.

So in the world of quantum physics, everything is probability. We could only say that electrons would be probably at a particular position.

That's why Bohr's model is not very accurate in describing the electrons in atoms. We would expect Bohr's model to be able to predict the location of electrons at any moment, but now we know electrons are just unpredictable.

Now we have to apply quantum physics to learn more about electrons in atoms.

Wave functions

It all starts with the wave functions. They are very complicated, and to be honest, we couldn't fully understand them and we have no idea how they are derived. Luckily, that doesn't matter for chemists.

So we'll just use some very simple words, and maybe too simple so that they're not 100% correct, to explain the most basics of wave functions and how they are related to the electrons in atoms.

Wave functions are mathematical equations that correlate the position of an electron and the probability of finding that electrons at that particular position. Wave function itself doesn't have physical representation, it is simply a value (\(\Psi\)) which is calculated using the position of the electron. However, if you take square of that value, \(\Psi^2\), it tells you the probability of finding the electron in that position.

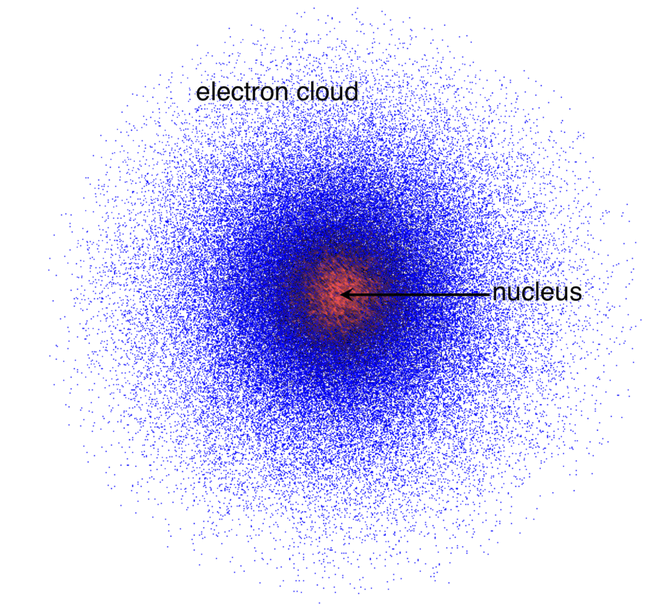
So if you vary the position and draw a dot when it is more than 95% probable to see the electron at that position, you'll get a map of probability density, or you can say, an electron cloud.

In the illustration above, the denser it is, the higher the probability that an electron would appear. It is generated by the wave function.

Inside the wave function, there're more than just the position variable. Some parameters are being used. These are called quantum number. There're four quanum numbers, namely principal quanum number (\(n\)), angular quantum number (\(l\)), magnetic quantum number (\(m\)), and spin quantum number (\(m_s\)). These numbers must be specific values in order for wave functions to have a solution. If you set a random quantum number, you may never see an electron appear, no matter what position it is at.

We could put it in this way: quantum numbers define an area in space where there could be a high probability of finding an electron. We call the area in space with a high probability of finding an electron the orbital.